2020년 발표된 “Denoising Diffusion Probabilistic Models” (DDPM)은 생성 모델 연구에 중요한 전환점을 제시한 논문입니다. 당시 Generative Adversarial Networks (GANs)는 훈련 불안정성과 모드 붕괴(mode collapse)와 같은 문제점에도 불구하고 높은 성능으로 인해 고품질 이미지 생성 분야에서 널리 사용되고 있었습니다. DDPM은 이러한 상황 속에서 Diffusion Model이라는 새로운 패러다임의 잠재력을 증명하며 후속 연구의 증가를 이끌어냈습니다.
DDPM 이전에도 Diffusion Model에 대한 아이디어는 있었지만, Variational Lower Bound (ELBO)를 최적화해야 하는 복잡한 학습 과정과 만족스럽지 못한 성능 때문에 주요 연구 흐름에서는 크게 주목받지 못했습니다. 하지만 Ho et al. (2020)의 DDPM은 모델 구조와 학습 목표(objective)에 대한 새로운 설계를 통해, Diffusion Model이 GAN에 필적하거나 이를 능가하는 고품질 이미지 생성이 가능함을 입증했습니다. 본 글에서는 DDPM의 방법론을 분석하고, 논문의 수식 전개 과정을 짚어보고자 합니다.
노이즈 확산과 복원 과정
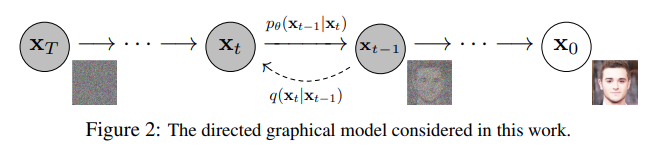
DDPM은 두 가지 마르코프 연쇄(Markov Chain) 과정에 기반합니다. 하나는 원본 데이터를 점진적으로 파괴하는 정방향 과정 (Forward Process)이고, 다른 하나는 파괴된 상태에서 원본을 복원하도록 학습하는 역방향 과정 (Reverse Process) 입니다.
정방향 과정 (Forward Process)
정방향 과정은 원본 데이터 $x_0$에 $T$ 타임스텝에 걸쳐 점진적으로 가우시안 노이즈를 추가하여, 최종적으로는 아무런 정보도 없는 순수 가우시안 노이즈 $x_T$로 변환하는 과정입니다. 이 과정은 모델이 학습하는 것이 아닌, 미리 정해진 규칙에 따라 진행되는 고정된 프로세스입니다. 각 단계 $t$에서의 변환은 다음과 같이 정의됩니다. (논문 Eq. 2)
\[q(x_t \mid x_{t-1}) = \mathcal{N}(x_t ; \sqrt{1 - \beta_t} x_{t-1}, \beta_t \mathbf{I})\]여기서 $\beta_t$는 $t$스텝에서 추가할 노이즈의 양을 조절하는 분산 스케줄(variance schedule)로, 미리 정의된 하이퍼파라미터입니다. DDPM에서는 $10^{-4}$에서 $0.02$까지 선형적으로 증가하는 스케줄을 사용했습니다. 즉, 초기 단계에서는 데이터의 구조를 거의 해치지 않는 작은 노이즈를 추가하고, 후반으로 갈수록 더 강한 노이즈를 주입하여 최종적으로 $x_T$가 $x_0$의 정보를 거의 잃은 표준 정규분포에 가까워지도록 합니다.
이 과정의 중요한 속성은, 매 스텝을 순차적으로 거치지 않고도 원본 $x_0$만 있다면 임의의 타임스텝 $t$의 노이즈 낀 데이터 $x_t$를 한 번에 얻을 수 있다는 점입니다. $\alpha_t = 1 - \beta_t$ 이고, $\bar{\alpha}_t = \prod_{s=1}^T \alpha_s$라고 정의하면, 재매개변수화 트릭(reparameterization trick)을 통해 $x_t$는 다음의 닫힌 형식(closed-form)으로 표현됩니다. (논문 Eq. 4)
\[x_t = \sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \text{where} \; \epsilon \sim \mathcal{N}(\mathbf{0, I})\]따라서 $q(x_t \mid x_0)$의 분포는 다음과 같습니다.
\[q(x_t \mid x_0) = \mathcal{N}(x_t ; \sqrt{\bar{\alpha}_t} x_0, (1-\bar{\alpha}_t) \mathbf{I})\]이 덕분에 모델 학습 시 전체 $T$ 스텝을 모두 시뮬레이션할 필요가 없습니다. 미니배치에서 뽑은 원본 이미지 $x_0$와 무작위로 고른 타임스텝 $t$만으로, 모델에 입력할 노이즈 데이터를 즉시 생성할 수 있습니다.
역방향 과정 (Reverse Process)
역방향 과정은 순수 노이즈 $x_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$에서 출발해, 정방향 과정을 거꾸로 따라가며 원본 데이터 분포의 샘플 $x_0$를 복원하는 것을 목표로 합니다. 이 과정은 신경망으로 모델링된 학습 가능한(learnable) 마르코프 연쇄입니다. (논문 Eq. 1)
\[p_\theta (x_{t-1} \mid x_t) = \mathcal{N}(x_{t-1} ; \mu_\theta (x_t, t), \Sigma_\theta (x_t, t))\]모델은 각 스텝 $t$에서 노이즈 낀 데이터 $x_t$를 입력받아, 이전 스텝 $x_{t-1}$의 분포를 결정하는 평균 $\mu_\theta$와 공분산 $\Sigma_\theta$를 예측하도록 학습됩니다.
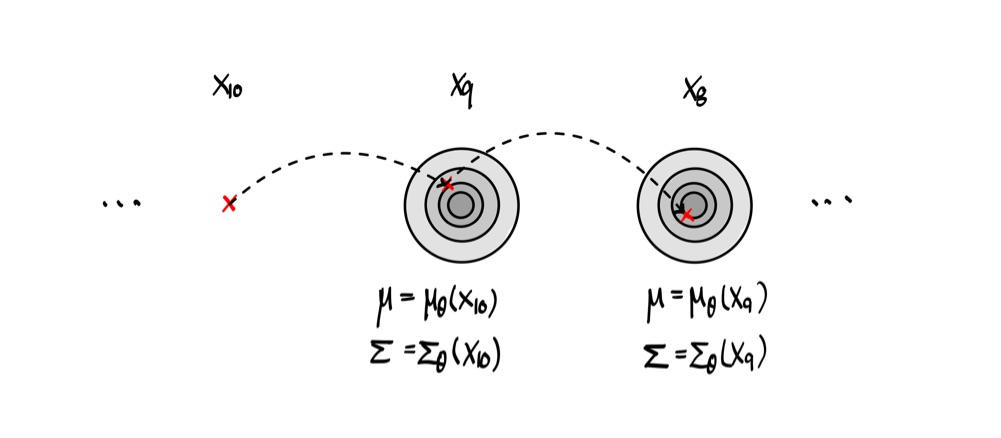
모델은 무엇을 보고 $\mu_\theta$를 예측해야 할까?
이상적인 목표는 정방향 과정의 실제 사후 확률 분포인 $q(x_{t-1} \mid x_t)$를 근사하는 것입니다. 하지만 이 분포를 계산하려면 $q(x_{t-1} \mid x_t) = \int q(x_{t-1} \mid x_t, x_0) q(x_0) d x_0$와 같이 전체 데이터 분포 $q(x_0)$에 대한 적분이 필요하므로 다루기 어렵습니다. 여기서 DDPM은 중요한 트릭을 사용하였습니다. 만약 원본 데이터 $x_0$가 조건으로 주어진다면, 이 사후 확률은 베이즈 정리에 의해 다루기 쉬운 형태로 유도될 수 있습니다. (논문 Eq. 6) $$ q(x_{t-1} \mid x_t, x_0) = \mathcal{N}(x_{t-1} ; \tilde{\mu}_t (x_t, x_0), \tilde{\beta}_t I) $$ 이 분포의 평균 $\tilde{\mu}_t$와 분산 $\beta_t$는 어떻게 유도가 될지, 논문에서는 생략된 이 과정을 살펴보겠습니다.
역방향 사후 확률 $q(x_{t-1} \mid x_t, x_0)$ 의 유도
베이즈 정리에 따라 $q(x_{t-1} \mid x_t, x_0)$는 다음과 같이 전개됩니다. $$ q(x_{t-1} \mid x_t, x_0) = q(x_t \mid x_{t-1}, x_0) \frac{q(x_{t-1} \mid x_0)}{q(x_t \mid x_0)} $$ 정방향 과정의 마르코프 성질에 의해 $q(x_t \mid x_{t-1}, x_0) = q(x_t \mid x_{t-1})$ 이므로, 각 항은 우리가 이미 알고 있는 가우시안 분포의 확률 밀도 함수(PDF)입니다. 가우시안 분포의 PDF는 $\exp$ 항으로 표현되므로, 이 식은 다음과 같이 지수부의 연산으로 변환됩니다. $$ \propto \exp \left( -\frac{1}{2} \left ( \frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}} x_0)^2}{1 - \bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_t}x_0)^2}{1-\bar{\alpha}_t} \right) \right) $$ 이 복잡한 지수부의 식을 $x_{t-1}$에 대한 이차식으로 정리하면, $x_{t-1}$이 따르는 새로운 가우시안 분포의 평균과 분산을 얻어낼 수 있습니다. 정리하게 되면, 분산 $\tilde{\beta}_t$와 평균 $\tilde{\mu}_t$는 다음과 같이 유도됩니다. (논문 Eq. 7) $$ \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t $$ $$ \tilde{\mu}_t(x_t, x_0) = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t $$ 이제 우리는 모델이 근사해야 하는 명확한 목표 $\tilde{\mu}_t$를 계산했습니다. 하지만 이 식은 여전히 학습 목표로 삼기에는 복잡하고, 결정적으로 학습 시점에는 알 수 없는 $x_0$를 포함합니다. 이 문제를 해결하기 위해 DDPM은 다시 한 번 목적 함수를 재설계합니다.예측 목표의 전환, 평균에서 노이즈로
DDPM의 기여 중 하나는 역방향 과정의 평균 $\mu_\theta$를 직접 예측하는 대신, 해당 스텝에서 추가된 노이즈만을 예측하도록 목표를 재매개변수화하고, 이에 맞춰 학습 목적 함수를 단순화한 것입니다.
앞서 유도한 $\tilde{\mu}_t$의 식을 다시 살펴보겠습니다. 여기에 정방향 과정의 속성인 $x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1-\bar{\alpha}_t} \epsilon)$을 대입하여 $x_0$를 소거하고 $x_t$와 $\epsilon$에 대한 식으로 정리하면, 다음과 같은 간결한 형태로 정리됩니다.
\[\tilde{\mu}_t(x_t, x_0) = \frac{1}{\sqrt{\alpha}_t} \left(x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon \right)\]이 식은 매우 중요한 사실을 내포합니다. 우리가 찾아야 할 이상적인 평균 $\tilde{\mu}_t$는 결국 $x_t$와 $\epsilon$의 선형 결합이라는 것입니다. $x_t$는 모델의 입력값이므로, 평균을 예측하는 문제는 곧 노이즈 $\epsilon$을 예측하는 문제와 동치가 됩니다. 즉, 학습 목표가 ‘이전 스텝의 깨끗한 이미지 평균’ 같은 복잡하고 추상적인 대상에서, ‘현재 이미지에 추가된 노이즈’라는 더 단순하고 직관적인 대상으로 바뀐 것입니다.
이 발견에 기반하여 저자들은 $\epsilon_\theta(x_t, t)$가 실제 노이즈 $\epsilon$을 예측하도록 설계합니다. 그리고 이를 이용해 모델이 예측할 평균 $\mu_\theta$를 다음과 같이 재구성합니다. (논문 Eq. 11)
\[\mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t) \right)\]이러한 재매개변수화는 Variational Lower Bound (ELBO)를 크게 단순화하는 효과를 가져옵니다. 복잡한 KL Divergence 항들이 정리되어, 최종적으로 다음과 같은 매우 직관적이고 간단한 형태의 목적 함수가 제안됩니다. (논문 Eq. 14)
\[L_{simple}(\theta) := \mathbb{E}_{t, x_0, \epsilon} \left[ \| \epsilon - \epsilon_\theta (\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) \|^2 \right]\]이 목적 함수는 “(1) 원본 이미지 $x_0$와 랜덤 타임스텝 $t$를 고르고, 해당 스텝의 노이즈 낀 이미지 $x_t$를 만든다. (2) 모델 $\epsilon_\theta$가 $x_t$와 $t$를 보고 우리가 주입한 실제 노이즈 $\epsilon$을 얼마나 잘 맞추는지 L2 Loss로 측정한다”는 직관적인 의미를 갖습니다. 이 단순화된 목적 함수는 DDPM의 성공에 결정적인 역할을 하였습니다.
실험 결과 및 평가
DDPM은 CIFAR-10, LSUN, CelebA-HQ 등 다양한 데이터셋에서 당시 SOTA 생성 모델들과의 성능을 비교했습니다. 특히 Unconditional CIFAR-10 데이터셋에서 Inception Score 9.46, FID 3.17을 달성하며, 당시 최고 수준의 GAN 모델들과 대등하거나 우월한 성능을 보였습니다.

이는 Diffusion Model이 고품질 이미지 생성에 매우 효과적인 inductive bias를 가지고 있음을 시사합니다. 다만, 샘플링 과정에서 수천 번의 순차적인 네트워크 연산이 필요하여 GAN에 비해 샘플링 속도가 현저히 느리다는 단점이 지적되었습니다.
결론
DDPM은 다루기 어려웠던 역방향 과정의 사후 확률($q$)이라는 이론적 목표를, ‘노이즈 예측’이라는 직관적인 문제로 재정의하고, 이를 효과적으로 학습할 수 있는 단순화된 목적 함수를 제안함으로써 Diffusion Model의 잠재력을 크게 향상시킨 중요한 연구입니다. 이 논문이 제시한 명확한 프레임워크와 성능은 이후 샘플링 속도 개선(DDIM), 조건부 생성, 텍스트-이미지 변환 등 수많은 후속 연구의 토대가 되었으며, 오늘날에도 생성 AI 발전에 크게 기여한 핵심 논문으로 평가됩니다.



Start the conversation