복소수와 오일러 공식 - 테일러 급수로 풀어보는 간단한 이해
1. 테일러 급수와 맥클로린 시리즈
먼저, 테일러 급수와 맥클로린 시리즈가 무엇인지 알아보겠습니다.
테일러 급수란?
어떤 복잡한 함수도 특정 점 주변에서 다항식으로 근사할 수 있습니다. 이때 사용되는 방법이 바로 테일러 급수입니다. 예를 들어, $f(x)$ 라는 함수가 있을 때, 이 함수를 아래와 같은 무한한 다항식으로 표현할 수 있습니다.
\[f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots\]이때 함수 $f(x)$ 의 도함수(미분)를 계산한 후 특정 점 $a$ 에서의 값을 구하여, 그 함수의 값과 변화율을 근사적으로 표현할 수 있습니다.
맥클로린 시리즈란?
맥클로린 시리즈는 테일러 급수의 특별한 경우로, 특정 점 $a$ 를 0으로 설정한 테일러 급수입니다. 즉, 함수 $f(x)$ 를 $x = 0$에서 전개한 것입니다.
\[f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \cdots\]쉽게 말해, $a = 0$ 일 때 테일러 급수를 사용하는 경우를 맥클로린 시리즈라고 부릅니다.
2. 복소수는 왜 필요할까?
복소수는 우리가 실수만으로 해결할 수 없는 문제를 해결해줍니다. 예를 들어, 실수 범위에서 (\sqrt{-1}) 같은 값을 계산할 수 없지만, 복소수를 도입하면 $j = \sqrt{-1}$ 로 정의하고 이런 문제를 해결할 수 있습니다. 복소수는 전기 회로 분석, 신호 처리, 물리학 등 다양한 분야에서 매우 유용하게 사용됩니다.
복소수는 복소평면에서 두 가지 성분(실수 부분과 허수 부분)으로 나타낼 수 있습니다. 이 두 성분을 이용하면 다양한 문제를 쉽게 시각화하고 계산할 수 있습니다. 오일러 공식 같은 것도 복소수를 사용하면 아주 깔끔하게 표현할 수 있습니다.
3. 오일러 공식
오일러 공식은 다음과 같은 식으로 표현됩니다:
\[e^{j\theta} = \cos\theta + j\sin\theta\]이 공식은 복소수와 삼각함수의 관계를 보여주는 놀라운 수식입니다. 이제 이 공식을 증명하기 위해 테일러 급수를 사용해보겠습니다.
테일러 급수로 오일러 공식 증명하기
테일러 급수를 사용하여 $e^{j\theta}$ 를 전개해보면, 다음과 같은 식이 나옵니다.
\[e^{j\theta} = 1 + j\theta + \frac{j^2}{2!}\theta^2 + \frac{j^3}{3!}\theta^3 + \cdots\]여기서 $j^2 = -1$ 이라는 성질을 사용하면 식을 정리할 수 있습니다.
\[e^{j\theta} = 1 + j\theta - \frac{1}{2!}\theta^2 - \frac{j}{3!}\theta^3 + \cdots\]위 식을 살펴보면 실수 부분과 허수 부분으로 나눌 수 있습니다.
- 실수 부분: $1 - \frac{1}{2!}\theta^2 + \frac{1}{4!}\theta^4 - \cdots$ → 이것은 $\cos\theta$의 테일러 급수입니다.
- 허수 부분: $j\left(\theta - \frac{1}{3!}\theta^3 + \frac{1}{5!}\theta^5 - \cdots \right)$ → 이것은 $j\sin\theta$의 테일러 급수입니다.
따라서, $e^{j\theta} = \cos\theta + j\sin\theta$ 라는 오일러 공식을 증명할 수 있습니다.
4. 복소평면과 오일러 공식의 의미
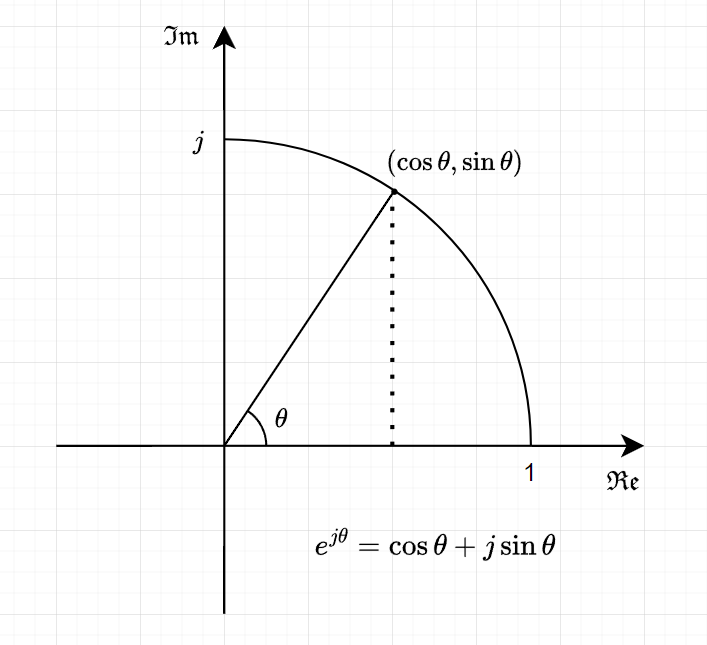
복소평면은 실수축과 허수축을 함께 나타낸 좌표평면이라고 생각할 수 있습니다. 오일러 공식에 나오는 $e^{j\theta}$ 는 복소평면에서 반지름이 1인 원 위의 점을 나타냅니다. 각도 $\theta$ 에 따라 점이 움직이며, 그 좌표는 $(\cos\theta, \sin\theta)$ 로 나타낼 수 있습니다.
여기에 복소수의 크기 $r$ 을 곱하면, 복소평면의 모든 점을 표현할 수 있습니다. 즉, $re^{j\theta}$ 는 반지름이 $r$ 인 원 위의 점을 의미하게 됩니다.
5. 요약
- 테일러 급수는 복잡한 함수를 다항식으로 근사하는 방법이고, 맥클로린 시리즈는 이를 $x = 0$ 에서 전개한 특별한 경우입니다.
- 오일러 공식은 복소수와 삼각함수의 관계를 보여주며, 이를 테일러 급수를 통해 증명할 수 있습니다.
- 복소평면에서 오일러 공식은 특정 원 위의 점을 표현하며, 그 좌표는 $(\cos\theta, \sin\theta)$ 로 나타낼 수 있습니다.