Table of Contents
분류 문제의 손실함수로 많이 쓰이는 cross entropy. 오늘은 이것이 무엇인지, 그리고 확률의 기초부터 정보이론을 거쳐 KL divergence와 어떤 관계를 갖는지까지 살펴보려고 한다. 최근 들어 어떤 공부를 하든지 이해만 되는 수준에 머무르지 않고, 끝내 다시 내 언어로 표현할 수 있어야 완전히 자신의 지식으로 체득하는 것이라는 생각을 많이 하게 되었다. 면접을 준비하거나 다른 사람들에게 배운 지식을 전달할 때도, 본인이 이해한 바를 쉽게 풀어 설명할 수 있으면 큰 도움이 되는 것을 느꼈다.
Proability distribution
앞으로 등장할 개념에서 확률분포(probability distribution)는 계속해서 나타날 것이므로 이 개념을 먼저 분명히 짚고 넘어가자. 확률분포는 확률변수가 특정 값을 가질 때의 확률을 나타낸 것이며, 크게 이산확률분포와 연속확률분포로 나눌 수 있다. 이 구분은 확률변수가 취할 수 있는 값이 이산적(discrete)인지 연속적(continuous)인지에 따라 정해진다.
확률변수란 어떤 사건(어떤 실험에서 관측되는 결과나 그 결과의 집합)을 수치로 대응시킨 값이다. 예로 “동전의 앞면”을 1로, “동전의 뒷면”을 2로 표현하는 것과 같다.
예를 들어, 주사위를 던질 때 가능한 결과는 1, 2, 3, 4, 5, 6의 6가지로 이산적이면서 유한하다. 매우 공정한 주사위를 아주 많이 던졌을 때, 각 눈이 나올 확률은 동일하며 모두 1/6로 수렴한다. 반면, 한 사람을 무작위로 뽑아 몸무게를 살펴보는 상황을 생각해보자. 그 사람의 몸무게는 50kg, 85kg와 같이 특정 정수 값으로 표현할 수도 있지만, 실제로는 50.142…kg, 85.10029kg처럼 연속적이고 무한히 다양한 값으로 나타낼 수 있다. 이처럼 값이 연속적이고 무한히 많은 경우는 연속확률분포에 속한다.
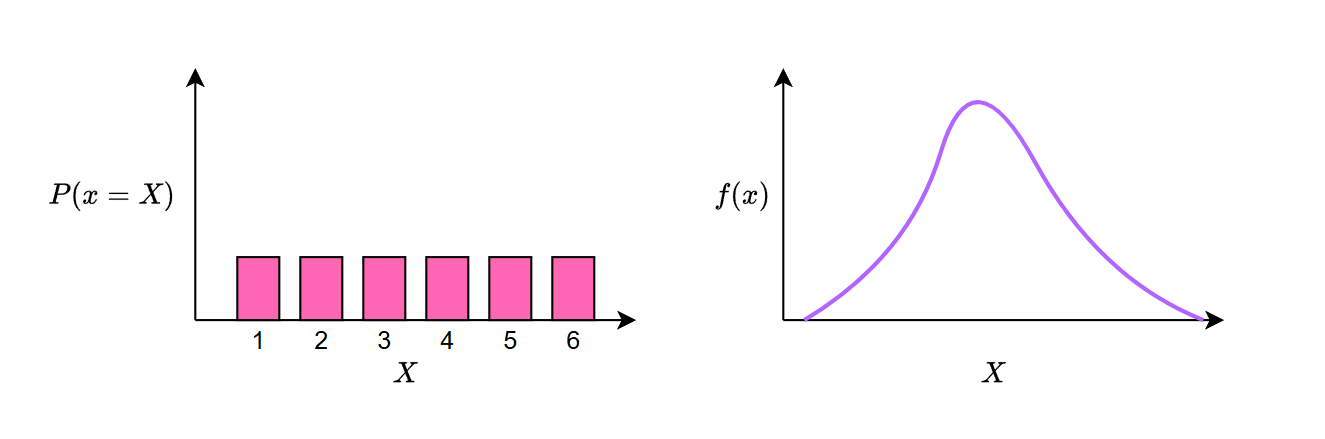이산확률분포와 연속확률분포
Entropy
Cross entropy를 제대로 이해하기 전에, 정보이론에서 중요한 개념인 entropy를 먼저 알아보자. 엔트로피는 정보의 불확실성을 나타내는 측도(measure)로, 어떤 사건이 일어나기 “어려울수록” 정보량이 크고, 그로 인한 놀람(surprise)의 정도가 크다는 의미를 담고 있다.
예를 들어, 내가 산 로또가 1등에 당첨되는 사건을 생각해보자. 발생 확률이 아주 낮기 때문에 이 사건에 해당하는 엔트로피는 매우 높다. 이런 희박한 사건이 실제로 발생하면 우리는 크게 놀라고, 이를 통해 많은 정보를 얻었다고 할 수 있다. 즉, 엔트로피를 ‘놀람의 정도’ 혹은 ‘희귀한 사건으로부터 얻는 정보량’이라 생각할 수 있다. 다음은 엔트로피를 계산하는 수식이다:
\[H(P) = -\sum_{x \in X} P(x) \log P(x)\]Information content
정보이론에서 한 사건의 정보량은 $-\log P(x)$로 정의한다. 발생할 확률이 낮을수록 그만큼 더 많은 정보를 가지고 있다는 것은 직관적으로 이해할 수 있다. 그러나 왜 $\log$와 음수를 취하는지 이해해봐야 한다. Shannon’s information theory에 의하면 정보량은 아래의 3가지 성질을 모두 만족해야 한다:
- 확률이 낮을 수록 정보량이 커야한다.
- 독립적인 사건의 정보량은 덧셈으로 계산되어야 한다.
- 확률이 1인 사건 (반드시 발생하는 사건)의 정보량은 0이다.
위 성질을 모두 만족하는 것이 $-\log$ 함수이기에 정보량을 측정하는 수식에 음의 로그가 포함되어 있다. 이제 엔트로피 식에서 정보량이 들어가는 이유가 조금 더 명확해진다. 엔트로피 식은 결국 전체 확률분포 상에서의 정보량을 평균적으로 계산하는 값인데, 여기서 평균을 내기 위해 기대값을 사용한다.
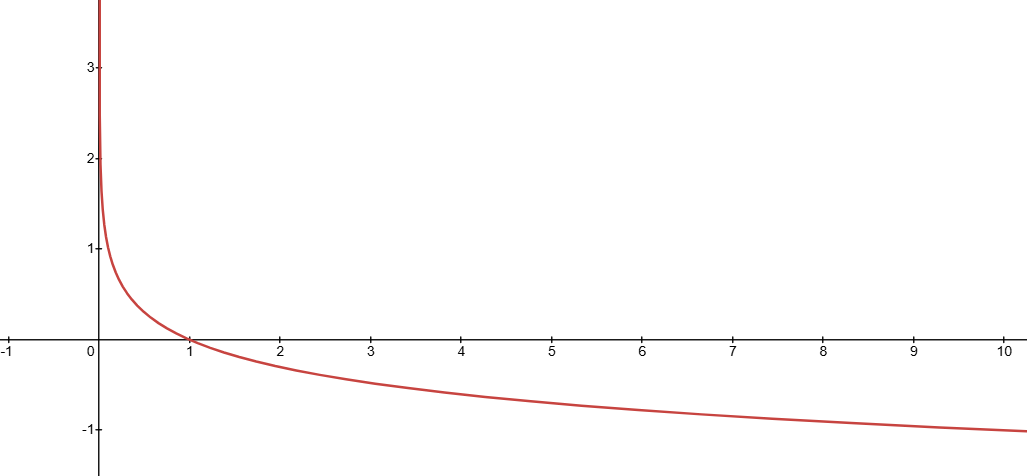Negative log function
Expectation
지금까지 살펴본 것은 어떤 실험(예: 주사위 던지기)중 하나의 사건(예: 주사위 눈이 4인 사건)만 보았다. 하지만 확률분포에서의 엔트로피는 일어날 수 있는 모든 사건들을 고려해야한다. 그렇기 때문에 각 사건의 정보량을 어떻게 보면 평균을 취하여 전체 대표값을 계산해야 하는데, 여기서 기댓값을 사용하게 된다.
기댓값은 평균과 혼용되어 사용되고 있지만 그 차이를 알아야 한다. 평균은 관측된 결과에 대한 산술평균을 계산하는 것이고, 기댓값은 관측되지 않은 결과, 확률분포만 보고 평균이 어떨지 예측하는 것이다. 그리고 기댓값의 수식은 다음과 같다:
\[\mathbb{E}[x] = \sum_{x \in X} P(x) \cdot x\]그러나 우리가 구하고 싶은 것은 각 사건의 정보량에 대한 기댓값이기 때문에 $x$대신 정보량 $I(x)$를 삽입한다. 이렇게 됨으로써 엔트로피의 수식과 같아진 것이며 “확률분포의 정보량에 대한 기댓값”을 의미한다고 해석할 수 있게 되었다. 즉 어떤 확률분포가 주어진다면 평균적으로 $\alpha$ 만큼의 정보를 얻을 수 있겠구나! 로 해석되는 것이다.
\[\mathbb{E}[I(x)] = \sum_{x \in X} P(I) \cdot I(x) = -\sum_{x \in X} P(x) \log P(x)\]
Cross entropy
이제 cross가 붙은 cross entropy를 살펴보자. 단일한 확률분포에서의 엔트로피가 아니라, 두 개의 확률분포 $P$와 $Q$를 동시에 고려한다. 머신러닝에서 $P$는 실제 정답의 확률분포, $Q$는 모델이 예측한 확률분포로 해석할 수 있다. Cross entropy는 다음과 같은 식으로 정의된다.
\[H(P, Q) = -\sum_{x \in X} P(x)\log Q(x)\]앞서 본 엔트로피 식과 매우 유사하나, 내부에 등장하는 로그의 인자가 $P(x)$가 아닌 $Q(x)$라는 점이 다르다. Cross entropy를 손실함수로 사용하는 이유는, 모델이 예측한 분포 $Q$가 실제 정답 분포 $P$와 얼마나 다른지 측정하고, 이를 최소화하면서 모델을 최적화하기 위해서다. 쉽게 예를 들어보자:
\[\begin{aligned} Q(x_1) &= 0.0001 \qquad I(x_1) = -\log Q(x_1) = 4 \\ Q(x_2) &= 0.9999 \qquad I(x_2) = -\log Q(x_2) = 0.0000434 \end{aligned}\]만약 실제 정답 분포 $P$가 $x_1$에 대해 높은 확률을 할당한다면(예: $P(x_1)=1$), cross entropy 값은 커져버린다. 모델이 틀린 곳($Q(x_1)$)에 높은 정보를 갖게 됐기 때문이다. 결국 cross entropy를 줄이고 싶다면 $Q$를 $P$에 가깝게 만들어야 한다. 즉, $P=Q$일 때 cross entropy가 최소가 된다. 여기서 $P=Q$는 모델이 정답을 완벽히 예측하는 상태다. 실제 분류문제에서는 정답 클래스에 확률을 1에 가깝게 예측할수록 cross entropy 값이 낮아진다.
Kullback-Leibler divergence
Cross entropy $H(P, Q)$는 $P=Q$ 일 때 최솟값을 갖는다. 이때 그 최솟값은 $H(P)$와 같으며, 따라서 $H(P, Q)$는 다음과 같이 재표현할 수 있다.
\[H(P, Q) = H(P) + Error\]위 식의 에러를 우리는 쿨백-라이블러 발산 (KL Divergence)라고 하며, 두 확률분포 $P$와 $Q$ 사이의 차이를 측정하는 값이다. 즉, KL Divergence는 cross entropy에서 실제 엔트로피 $H(P)$를 제외한 나머지 “추가 비용”이라고 해석할 수 있다. $D_{KL}(P\Vert Q)$는 두 분포가 얼마나 다른지를 나타내며, 값이 0이면 두 분포가 완전히 동일함을 의미한다.
\[\begin{aligned} D_{KL}(P\Vert Q) &= H(P, Q) - H(P) \\ &= -\sum_{x \in X} P(x)\log Q(x) + \sum_{x \in X} P(x) \log P(x) \\ &= \sum_{x \in X} P(x) (\log P(x) - \log Q(x)) = \sum_{x \in X}P(x) \frac{P(x)}{Q(x)} \end{aligned}\]Summary
지금까지 확률분포의 개념에서 출발해 정보량, 엔트로피, 그리고 크로스 엔트로피까지 차근차근 살펴보았다. 한 사건의 발생확률이 낮을수록 그 사건은 더 많은 정보를 담고 있으며, 이 정보량을 기반으로 전체 분포의 불확실성을 나타낸 것이 엔트로피다. 그리고 두 확률분포 $P$(정답)와 $Q$(모델 예측)를 고려할 때, $Q$가 $P$와 얼마나 다른지를 측정하기 위해 cross entropy를 사용할 수 있다. 이때 cross entropy와 엔트로피의 차이가 바로 KL Divergence이며, 이것은 두 분포 사이의 ‘오차’를 의미한다.
정리하자면, 분류 문제의 손실함수로 많이 사용되는 cross entropy는 실제 정답 분포를 기준으로 모델 예측 분포가 얼마나 비슷하거나 다른지를 수치화하는 척도다. 이를 통해 모델은 정답에 가까워지도록 학습하고, 그 과정에서 KL Divergence는 점점 줄어들어 두 분포가 일치하는 방향으로 나아가게 된다.
Start the conversation