Discrete Time Fourier Transfrom (DTFT)

Discrete Time Fourier Transform은 이산 신호를
주파수 영역의 신호로 변환하는 도구이다.

우리 주변의 신호는 음성, 음악 그리고 디지털 영상 등 다양한 형태로 존재한다. 이러한 신호를 분석하고 처리하는데 있어 주파수 영역에서의 표현은 매우 중요하게 작용한다. 특히, 디지털 신호 처리에서 이산 신호를 다루기 위해 Discrete Time Fourier Transform (DTFT)라는 강력한 도구가 사용된다. 이 글에서는 DTFT를 이해하기 위해 필요한 기본 개념부터 차근차근 살펴보려고 한다.

Discrete Time Signal

https://www.javatpoint.com/discrete-time-signals-in-discrete-mathematics

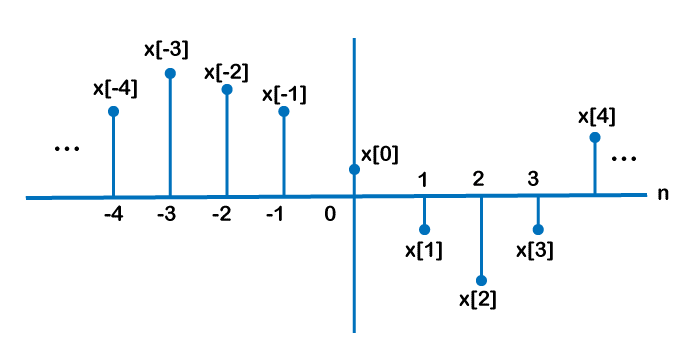
이산 신호란 연속 신호와 달리 특정 시간 간격에서만 정의되는 신호를 말한다. 예를 들어, 디지털 오디오 데이터는 샘플링된 이산 신호의 대표적인 예이다. 이산 신호는 수식으로 보통 $x[n]$과 같은 형태로 표현되며, 여기서 $n$은 정수로 나타내는 시간 축의 인덱스를 의미한다.

---

Discrete Time Fourier Series (DTFS)

이전글에서 살펴본 것 처럼, Fourier Series는 주기적인 신호를 주파수 영역의 기본 조화파들의 합으로 표현하는 방법이다. 이를 수식으로 나타내면 다음과 같다:

\[x[n] = \sum_{k=0}^{N-1} X[k] \cdot e^{j \frac{2\pi}{N} kn}\]

• $x[n]$: 주기 이산 신호
• $X[k]$: $x[n]$ 의 DTFS 계수, 즉 해당 주파수 성분의 크기와 위상 정보
• $N$: 신호의 주기
• $k$: 이산 주파수 인덱스

주기를 가지는 이산신호는 $N$개의 값들이 반복되므로, 주파수를 표현할 때 원 한 바퀴($2\pi$)를 $N$으로 나누어 작성한다.

---

DTFS Coefficient의 유도

복소 지수 함수의 직교 성질을 활용해 각 주파수 성분의 계수 $X[k]$를 유도할 수 있다. 두 복소지수 함수 $e^{j \frac{2\pi}{N} kn}$과 $e^{j \frac{2\pi}{N} mn}$의 내적을 계산하면:

• $m \neq k$: $\sum_{n=0}^{N-1} e^{j \frac{2\pi}{N} (k-m)n} = 0$
• $m = k$: $\sum_{n=0}^{N-1} e^{j \frac{2\pi}{N} (k-m)n} = N$

이를 기반으로 각 주파수 성분의 크기를 다음과 같이 계산할 수 있다:

\[X[k] = \frac{1}{N} \sum_{n=0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N}kn}\]

---

Discrete Time Fourier Transform (DTFT)

DTFS는 주기적인 이산 신호를 분석하는 데 사용된다. 그렇다면 주기가 없는 이산 신호는 어떻게 분석할 수 있을까? 여기서 DTFT가 등장한다. 주기 신호의 주기를 무한대로 확장하면 $N \rightarrow \infty$가 되고, 주파수 인덱스 $k$는 연속 주파수 $\omega$로 변환된다. 이때 DTFT는 다음과 같이 정의된다:

\[\lim_{N \rightarrow \infty} X[n] = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{n=0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N} kn}\] \[X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n]\cdot e^{-j\omega n}\]

여기서 $X(e^{j\omega})$는 연속 주파수 $\omega$에 대한 주파수 성분을 나타낸다. DTFT는 모든 시간 축에서의 신호 $x[n]$의 정보를 주파수 영역으로 변환하며, 이를 통해 신호의 주파수 특성을 확인할 수 있다.

주파수 대역에서의 주기성
DTFT는 주파수 대역에서 주기성을 갖는다. 이는 $X(e^{j\omega})$가 $\omega + 2\pi$에서 반복되는 성질에서 확인할 수 있다.

\[X(e^{j(\omega + 2\pi)}) = \sum_{n=-\infty}^{\infty} x[n] \cdot e^{-j(\omega + 2\pi) n} = X(e^{j\omega})\]

---

inverse Discrete Time Fourier Transform (iDTFT)

DTFT의 역변환은 주파수 영역의 정보를 시간 영역으로 복원하는데 사용된다. 이를 위해 DTFS의 식에서 시작해 리만 합을 적용하면 다음과 같이 유도된다:

\[\begin{aligned} x[n] &= \sum_{k=<N>}X[k] e^{j\frac{2\pi}{N}kn} \\ &= \frac{1}{2\pi} \sum_{k=<N>} N\cdot X[k] \cdot e^{j\frac{2\pi}{N}kn} \cdot \frac{2\pi}{N} \end{aligned}\]

위 식에서 복소 지수 함수의 $\frac{2\pi}{N}k$ 는 연속적인 값인 $\omega$ 로 변화하고, 가장 마지막 $\frac{2\pi}{N}$ 역시 미소변화량 $\Delta \omega$ 로 바뀐다. 이는 리만합과 같아져 전체 구간에 대한 적분으로 해석할 수 있게 된다.

\[\therefore x[n] = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(e^{j\omega}) e^{j\omega n} d\omega\]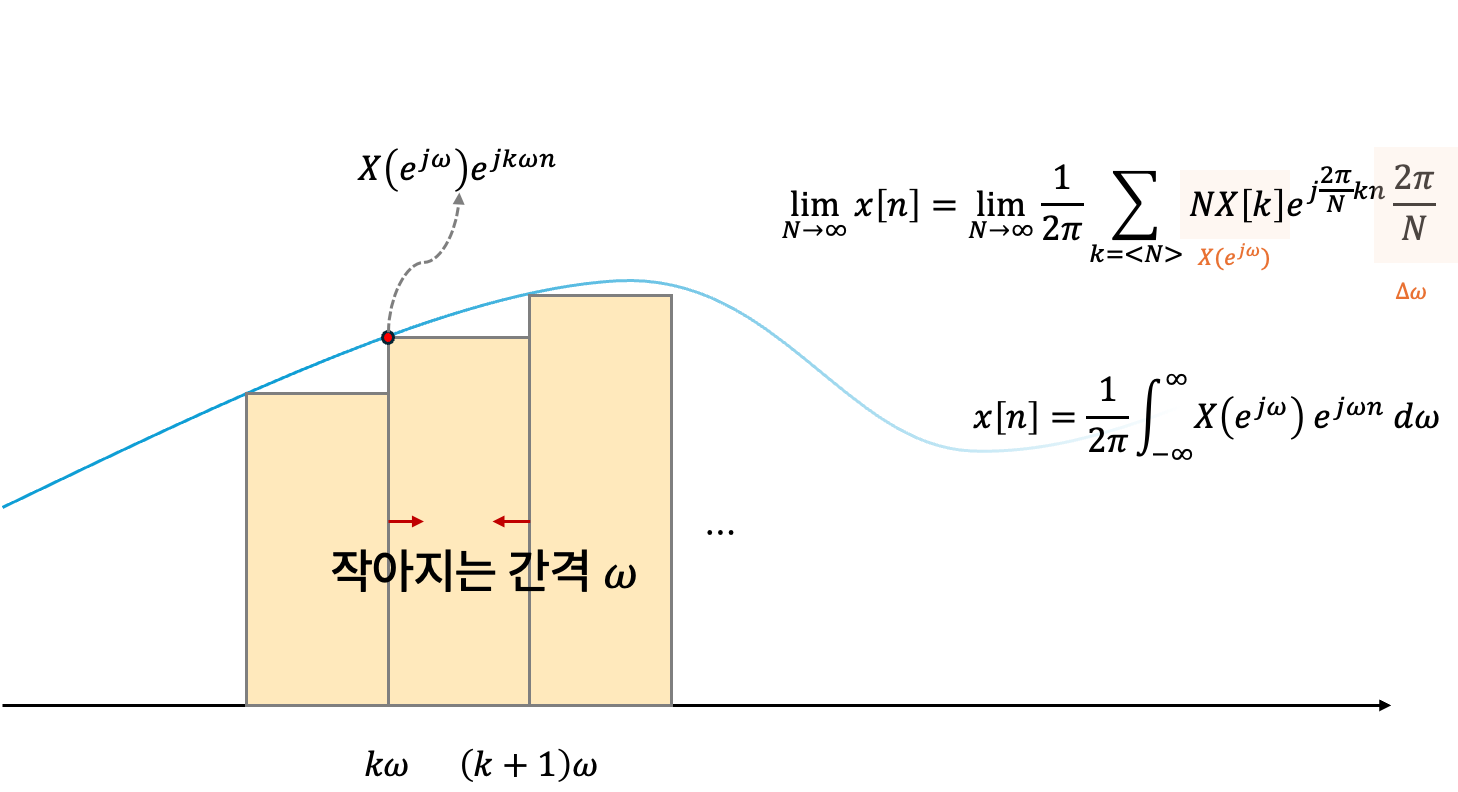

여기서 $X(e^{j\omega})$는 주파수 성분, $e^{j\omega n}$는 복원할 시간 축의 정보를 포함한다. 이를 통해 DTFT를 통해 얻은 주파수 정보를 다시 시간 영역으로 변환할 수 있다.

---

Example: DTFT of a cosine signal

임의의 코사인 이산 신호 함수가 존재할 때, 여기에 푸리에 변환을 적용한 결과는 어떻게 나오는지 살펴보자. 미리 말하자면, 이번 예제의 목적은 주기신호의 DTFT 결과는 임펄스 함수로 표현됨을 보이기 위함이다.

\[\begin{aligned} x[n] &= \cos (\omega_0 n) \\ &= \frac{1}{2}e^{j\omega_0 n} + \frac{1}{2}e^{-j\omega_0 n} \end{aligned}\]

오일러 공식에 의하면, 코사인 함수는 오직 2개의 정현파로만 구성되어 있어 2개의 주파수 성분만 가지고 있음을 볼 수 있다. iDTFT의 정의를 적용하여 그 때의 주파수는 $\pm \omega_0$ 일 때인 것을 도출하게 된다.

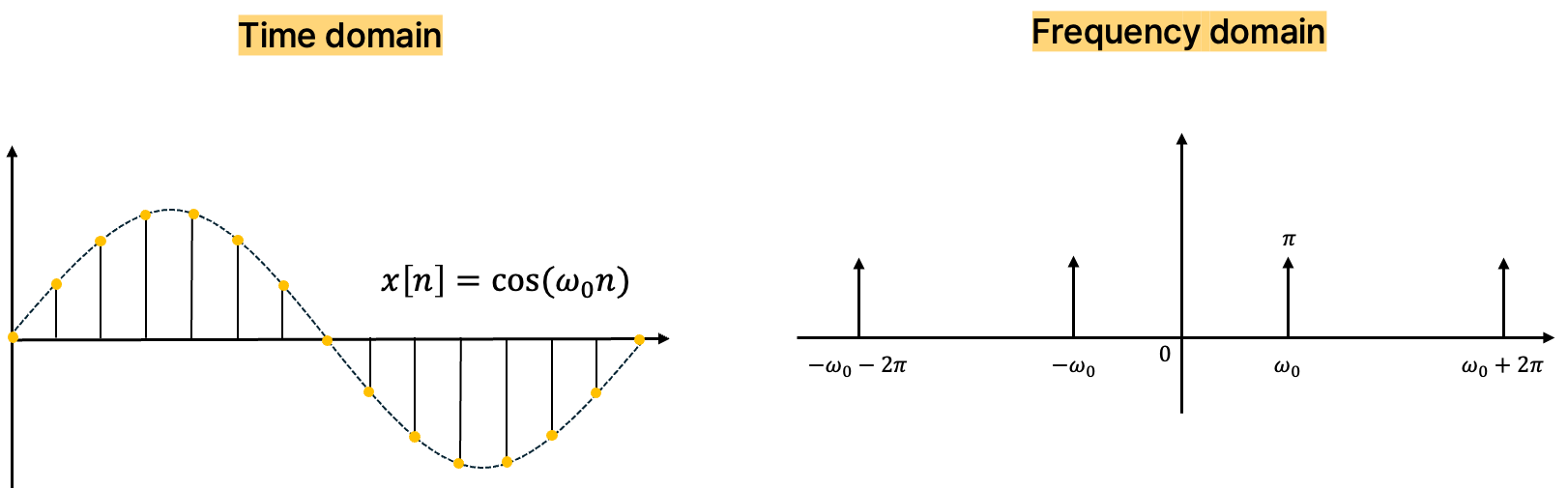Dicrete Time Fourier Transform of a cosine signal

---

Summary

이번 글에서는 DTFT를 이해하기 위해 discrete time signal, discrete time fourier series에 대해서 알아보았다. Fourier series가 주기 신호를 분석하는데 사용된다면, Fourier transform은 비주기 신호를 DTFT는 이산 비주기 신호를 주파수 영역에서 분석하는데 사용이 된다. 또한, fourier coefficient 계수의 유도 과정을 조화파의 직교성을 활용하여 수식적으로 확인하였다.

이러한 개념들은 디지털 신호 처리의 기본이 되며, 오디오 분석, 영상 처리, 그리고 통신 시스템등 다양한 분야에서 응용이 된다. DTFT는 단순한 수학적 정의를 넘어 우리가 일상에서 사용하는 디지털 기술의 핵심 원리를 설명해주는 매우 중요한 개념이라고 생각된다.