Matrix Similarity and Basis Transformations

We say that matrix $A$ and $B$ are similar if the following equation holds for some invertible matrix $Q$: $A = Q^{-1}BQ$

In a previous post about machine learning, we explored the concept of linear transformations. A linear transformation can be thought of as a bridge connecting vector spaces. But what happens when we stay within the same vector space but change its basis? This is where the concept of a change of coordinates matrix comes into play. Let’s delve into this idea and its geometric interpretation.

Change of coordinate matrix

To understand what a change of coordinate matrix is, consider the following example of a linear transformation:

Under this transformation, the equation $2x^2 - 4xy + 5y^2 = 1$, which describes an ellipse, transforms into $(x^\prime)^2 + 6(y^\prime)^2 = 1$, a simpler representation of an ellipse in the new coordinate system. This illustrates how a linear transformation changes the basis of a vector space by stretching and rotating it while preserving its dimension.

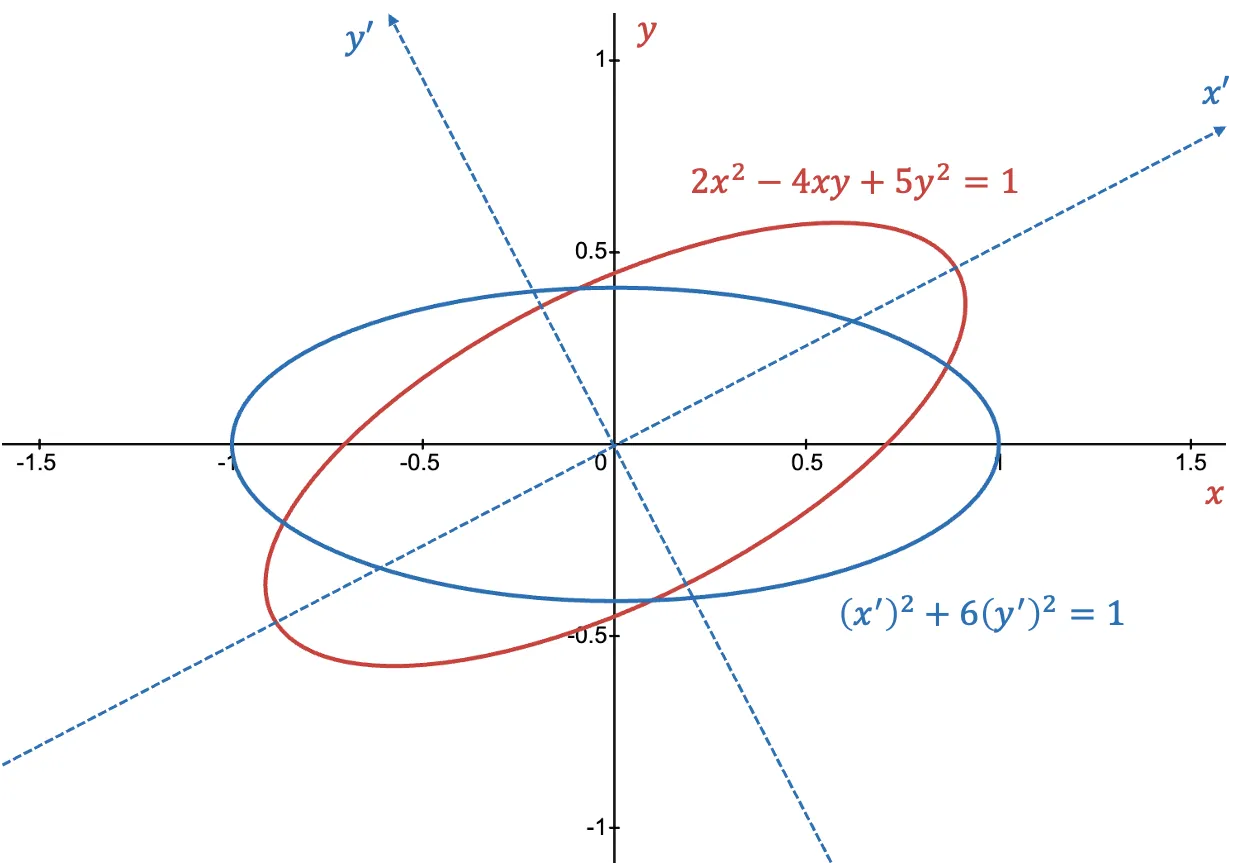Linear transformation applied to ellipse equations

Now, we can express this transformation mathematically by defining two bases, $\beta_1$ and $\beta_2$, for a vector space $V$. The transformation matrix can be written as $Q = [T]_{\beta_2}^{\beta_1}$, where $Q$ is the change of the coordinate matrix that relates the two bases. In general, for a vector $v$, we have the relationship:

Here, $Q$ is the linear transformation that maps the coordinates of $v$ in the $\beta^\prime$-basis to its coordinates in the $\beta^{\prime}$-basis. Since $Q$ preserves the vector space $V$, it must be invertible.

If the linear transformation does not change the vector space but only changes the basis, we call it a linear operator. For example, $[T]_\beta$ represents a linear transformation $T$ that preserves the basis $\beta$. The relationship between the linear operator in two different bases, $[T]_\beta$ and $[T]_{\beta^\prime}$, is given by:

Similar Matrix

How can we define matrix similarity? What does it mean for two matrices to be similar? We say that matrix $A, B \in \mathbb{R}^{n\times n}$ are similar if there exists an invertible matrix $Q$ such that:

This equation implies that the matrices $A$ and $B$ represent the same linear transformation but in different bases. In other words, the vector spaces spanned by $A$ and $B$ are the same, and the change of basis is facilitated by the matrix $Q$. Thus similarity provides another representation of a linear transformation with respect to different basis.

Properties of similar matrix

If the matrices $A, B \in \mathbb{R}^{n \times n}$ are similar, they exhibit the following properties:

1. Preservation of Eigenvalues

   The eigenvalues of similar matrices are the same, as shown by the character-istic polynomial. Let us apply the characteristic polynomial to matrix $B$:

   \[\begin{aligned} \det(B - \lambda I) &= \det(Q^{-1} AQ - \lambda I) \\ &= \det(Q^{-1}(A Q- \lambda Q)) \\ &= \det(Q^{-1}(A - \lambda I)Q) \\ &= \det(Q^{-1})\det(A - \lambda I) \det(Q) \\ &= \det(Q^{-1}Q)\det(A-\lambda I) \\ &= \det(A-\lambda I) \end{aligned}\]

   This demonstrates that the eigenvalues of $A$ and $B$ are identical.

2. Preservation of Rank

   Similar matrices have the same rank because the similar transformation does not alter the dimension of the vector space. Rank is an intrinsic property of the matrix and remains unchanged.

3. Same Trace

   The trace of similar matrices is equal. Using the cyclic property of the trace, $tr(AB) = tr(BA)$, we can show:

   \[tr(B)=tr(Q^{-1}AQ)=tr(Q^{-1}QA)=tr(A).\]

4. Same Determinant

   The determinant of similar matrices is also the same. This can be proven as follows:

   \[\begin{aligned} \det(B) &= \det(Q^{-1}AQ) \\&=\det(Q^{-1})\det(A)\det(Q) \\ &= \det(Q^{-1}Q)\det(A)\\ &= \det(I)\det(A) \\ &= \det(A) \end{aligned}\]

Summary

We’ve explored the concept of linear transformations that preserve the vector space, maintaining its dimension while potentially changing its basis. These transformations gave us the framework to define and understand similar matrices, along with their key properties.

In deep learning, linear transformations are ubiquitous. They allow models to view the same data from different perspectives by rotating and shifting the vector space. This process enables the extraction of diverse information from the data. In my opinion, this is one of the reasons why linear algebra is essential for deep learning—it provides the foundation to understand and expand our perspective on how models learn and process data.