Table of Contents
딥러닝을 공부하다 보면, ‘선형’이라는 단어를 꽤 자주 듣는 정도가 아닌 직간접적으로 항상 접하게 된다. 생각해보면, 실제 선형적인 것은 무엇이고, affine transformation이라고도 불리는 선형변환이란 무엇일까? 더 나아가, 행렬로 표현되는 선형변환이 기하학적으로 어떤 의미를 갖는지 살펴보자.
Linearity
선형대수학에서 선형변환이란 선형성(linearity)을 만족하는 변환을 의미한다. 여기서 선형이라는 것은 무엇을 의미할까? 어떠한 것이 선형적이다라고 한다면 2가지 성질을 반드시 만족해야 한다. 하나는 additivity(가법성)이고, 다른 하나는 homogeneity(동차성)이다. 각각 벡터의 덧셈과 스칼라 곱셈에 대해 변환이 아래의 수식을 만족해야 한다는 의미이다.
어떤 벡터공간 $V$ 에서 임의로 두 벡터 $x_1, x_2$ 를 선택했다고 하자. 이때 각 벡터에 선형변환 $T$ 를 적용한다면 다음 두 가지 성질을 만족해야 한다.
\[T(x_1+x_2) = T(x_1)+T(x_2) \tag{additivity}\] \[T(cx_1) = cT(x_1) \tag{homogeneity}\]위 수식은 변환 $T$를 벡터에 적용할 때, 개별적으로 변환한 뒤 더한 결과와 먼저 더한 뒤 변환한 결과가 동일해야 함을 나타낸다. 두 번째 수식은 임의의 상수 $c$에 대해 스칼라 배가 유지되어야 함을 의미한다.
Vector space
선형변환은 하나의 벡터공간에서 다른 벡터공간으로 벡터를 이동시키는 역할을 한다. 이를 이해하기 쉽게 비유하자면, $A$ 세상에 사는 $a$ 라는 사람이 특정 포털(선형변환)을 거쳐 $B$ 세상으로 이동하는 것과 같다. 여기서 중요한 점은 $A$ 세상과 $B$ 세상이 “선형적” 관계를 갖는다는 것이다.
조금 더 심화하여, 벡터공간을 이루는 주요 구성요소는 기저(basis)이다. 기저는 해당 벡터공간의 모든 원소를 span(생성)할 수 있는 최소한의 벡터 집합이다. 이를 건축물의 뼈대와 비유할 수 있다. 선형변환은 이러한 기저를 기울이거나 늘리면서 새로운 기저를 생성하고, 이를 기반으로 새로운 벡터공간을 만드는 것이다. 즉, 선형변환 $T: V \rightarrow W$ 는 벡터공간 $V$의 뼈대가 되는 기저 $\beta$ 를 잘 기울이고 늘리거나 줄여 새로운 기저 $\gamma$ 를 만들어주는 연산이고, 이 $\gamma$ 라는 기저로 만든 벡터공간이 $V$ 가 되도록 하는 것이다.
Matrix
어떤 선형변환 $T(x, y) = (x - y, 0)$ 을 고려해보자. 2차원 벡터공간 $V$에서 표현되던 좌표 $(x, y)$에 선형변환을 가했더니 다른쪽 벡터공간 $W$ 에서는 $(x-y, 0)$ 로 표현된다는 소리이다. 이것은 2차원에서 1차원 공간으로 벡터가 매핑된다는 것으로 그려볼 수 있다. 사실 위 연산은 행렬로서 나타낼 수 있다.
\[\begin{bmatrix}x \\ y \end{bmatrix} \begin{bmatrix}1 & -1 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix}x-y \\ 0 \end{bmatrix}\]Transformation에 해당되는 것은 중앙에 존재하는 행렬이다. 이전에 설명한 것과 같이 어떤 기저 $\beta$ 에서 다른 벡터공간의 기저 $\gamma$ 로 변환하는 연산으로 표현되기도 하기에 기호로 $[T]_\beta^\gamma$ 로 작성한다.
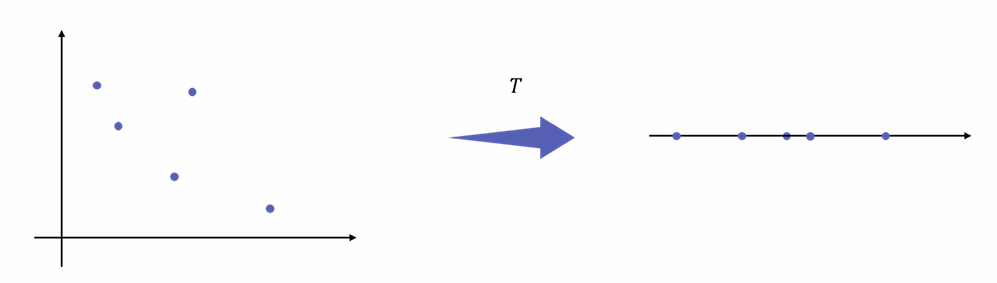 Sample linear transformation
Sample linear transformation
Inverse transformation
선형변환 $T$ 에 의해 다른 벡터공간으로 매핑된 벡터를 다시 원래 공간으로 되돌릴 수 있을까? 이 경우를 역변환(inverse transformation)이라 한다. 역변환이 가능하려면 변환 과정에서 일대일 대응(one-to-one correspondence)이 유지되어야 한다.
하지만 차원이 유지되는 경우, 즉 선형변환에 있어서 차원의 붕괴가 일어나지 않는 변환은 다시 되돌아 올 수 있는 역변환이 있다. 이 경우 우리는 선형변환 행렬 $A$에 있어서 역행렬 $A^{-1}$ 을 가질 수 있다고 말한다. 가장 직관적으로 집합으로서 이것을 이해해볼 수 있다.
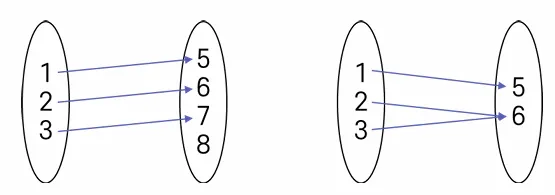
우측 그림에서 2와 3 모두 선형변환 $T$ 를 거쳤을 때 6에 대응되었다면, 6은 다시 되돌아갈 때 2로 가야할지 3으로 가야할지 모르는 상황이 발생된다. 이런 경우 역행렬(변환)을 가질 수 없다. 따라서, 역행렬이 존재하기 위한 조건 중 하나는 반드시 모든 벡터끼리 일대일대응을 유지해야하는 것이며, 이는 모든 차원이 그대로 유지되어야함을 내포한다.
$T: V \rightarrow W$ 를 공간의 이동이라면
다음과 같이 매우 추상적으로 비유해볼 수 있지 않을까?
 게임의 특성을 반영하면 위 변환은 사실 선형적이지 않다. (이해를 위한 예시일 뿐)
게임의 특성을 반영하면 위 변환은 사실 선형적이지 않다. (이해를 위한 예시일 뿐)
Summary
선형변환은 벡터공간 간의 이동을 담당하며, additivity와 homogeneity라는 두 가지 선형성을 만족하는 변환이다. 또한, 선형변환은 행렬로 나타낼 수 있으며, 이는 각 공간의 기저 간 관계를 연결하는 역할을 한다. 나아가, 연립방정식을 해결하는 과정도 벡터공간의 변환으로 시각화하며 이해할 수 있다.


Start the conversation