Table of Contents
이번 글은 지난 글: Understanding ANOVA에 이어 이원분산분석에 대해 다룬다. 두 개의 독립 변수를 동시에 고려하며, 상호작용 효과까지 분석하는 방법을 중심으로 설명한다.
Two-way ANOVA
식물을 키우는 실험에서 비료뿐만 아니라 흙의 종류도 동시에 바꿔가며 실험을 진행했다고 하자. 이 경우 각 표본 집단의 평균 차이를 어떻게 분석할 수 있을까? 이원분산분석은 일원분산분석의 확장이자 이러한 문제를 해결하는 방법이다. 일원분산분석과 마찬가지로, 이 기법은 ‘분산’을 활용하여 표본 평균 차이가 유의미한지를 검정한다.
독립 변수가 2개가 되면, 변수 간의 상호작용을 고려해야 한다. 비료를 3배 많이 주고, 흙도 3배 더 좋은 것으로 바꾼다고 해서 결과가 정확히 9배 좋아지지는 않을 것이다. 상호작용에 따라 결과가 더 좋아질 수도, 덜 좋아질 수도 있다. 이원분산분석은 이런 상호작용을 포함해 각 독립 변수가 결과에 미치는 영향을 분석하는 데 초점이 맞춰져 있다.

이원분산분석에서는 다음 세 가지를 확인할 수 있다:
- 비료가 식물 성장에 유의미한 차이를 보이는지.
- 흙이 식물 성장에 유의미한 차이를 보이는지.
- 비료와 흙 간의 상호작용이 식물 성장에 영향을 미쳤는지.
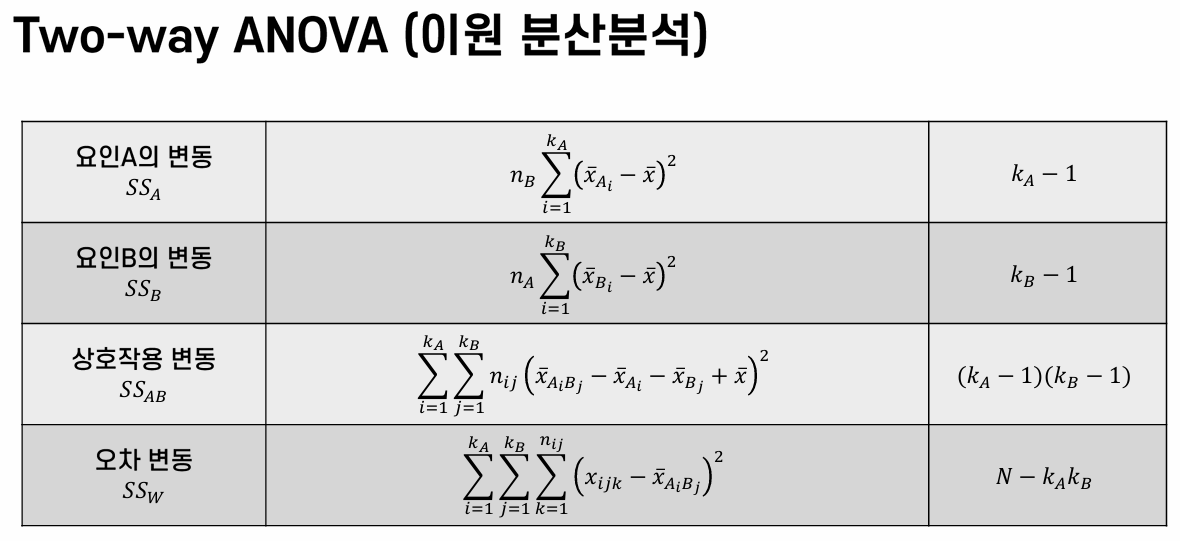
이를 위해, 독립 변수 A(비료), 독립 변수 B(흙), 그리고 두 변수의 상호작용(비료 × 흙)에 대한 분산을 각각 계산한다. 마지막으로, 오차에 대한 분산까지 포함하여 네 가지 분산 값을 분석한다. 수식은 아래와 같다:
\[SS_A = \sum_{i=1}^{k_A} n_i(\bar{x}_i - \bar{x})^2 \qquad SS_B = \sum_{j=1}^{k_B} n_j(\bar{x}_j - \bar{x})^2\] \[SS_{AB} = \sum_{i=1}^{k_A} \sum_{j=1}^{k_B} n_{ij} (\bar{x}_{ij} - \bar{x}_i - \bar{x}_j + \bar{x})^2 \qquad SS_E = \sum_{i=1}^{k_A} \sum_{j=1}^{k_B} \sum_{r=1}^{n_{ij}} (x_{ijr} - \bar{x})^2\]위 수식에서 $k_A$ 는 독립변수 A에 존재하는 카테고리의 수(e.g., 비료a, 비료b, 비료c)를 의미하며, $\bar{x}$ 는 전체 데이터의 평균값을 말한다. 상호작용에 대한 분산을 계산할 때, 각 독립변수에 대한 표본 평균을 빼주고 전체 평균을 더해주어 오직 상호작용과 관련된 정보만 남길 수 있도록 수식이 작성된 것이다. 분산의 계산 이후, 위에서 구한 각 표본에 대한 분산 값은 자유도로 나누어주어 평균 분산을 계산하게 된다.
| $SS_A$ | $SS_B$ | $SS_{AB}$ | $SS_E$ | |
|---|---|---|---|---|
| 자유도 | $k_A - 1$ | $k_B - 1$ | $(k_A-1)(k_B-1)$ | $N-k_Ak_B$ |
이후, 각 분산 값을 해당 자유도로 나누어 평균 분산($MS$)을 구하고, 이를 통해 f-value를 계산하여 각각의 독립 변수와 상호작용 효과의 유의미성을 판단한다.
\[\text{f-value}_A = \frac{\frac{SS_A}{k_A - 1}}{\frac{SS_E}{N-k_Ak_B}} = \frac{MS_A}{MS_E}\] \[\text{f-value}_B = \frac{\frac{SS_B}{k_B - 1}}{\frac{SS_E}{N-k_Ak_B}} = \frac{MS_B}{MS_E}\] \[\text{f-value}_{AB} = \frac{\frac{SS_{AB}}{(k_A - 1)(k_B - 1)}}{\frac{SS_E}{N-k_Ak_B}} = \frac{MS_{AB}}{MS_E}\]
Example: Two-way ANOVA
3개의 서로 다른 비료와 2개의 서로 다른 토양 조건에서 식물의 성장이 어떻게 변화하는지 관찰했다고 하자. 이 실험에서는 각 독립변수가 식물 성장에 유의미한 영향을 미쳤는지 확인하기 위해 이원 분산분석을 활용할 수 있다. 이때, 두 독립변수의 개별 효과뿐만 아니라, 두 변수 간의 상호작용 효과도 함께 검토해야 한다. 다음은 각 조건에서 측정된 데이터를 나타낸 표이다:
| 토양A | 토양B | |
|---|---|---|
| 비료A | 20, 21, 19 | 22, 23, 21 |
| 비료B | 30, 29, 31 | 32, 33, 31 |
| 비료C | 25, 24, 26 | 27, 28, 26 |
-
비료의 분산 계산
비료에 대한 각 그룹 평균은 $\bar{x}_{\text{A}} = 21$, $\bar{x}_{\text{B}} = 31$, $\bar{x}_{\text{C}} = 26$이며, 전체 평균은 $\bar{x} = 26$이다. 이를 기반으로 비료의 분산을 계산하면 다음과 같다:
\[SS_{\text{비료}} = 6(21-26)^2 + 6(31-26)^2 + 6(26-26)^2 = 300\] \[MS_{\text{비료}} = \frac{300}{3-1} = 150\] -
토양의 분산 계산
토양에 대한 각 그룹 평균은 $\bar{x}_{\text{토양A}} = 25$, $\bar{x}_{\text{토양B}} = 27$ 이다. 이를 기반으로 토양의 분산을 계산하면:
\[SS_{\text{토양}} = 9(25-26)^2 + 9(27-26)^2 = 18\] \[MS_{\text{토양}} = \frac{18}{2 - 1} = 18\] -
상호작용의 분산 계산
상호작용 분산은 두 독립 변수 간의 영향을 따로 계산한다. 실제로 위에서 언급한 수식을 따르면 \(SS_{\text{비료, 토양}} = 0\) 이 나오게 된다. 이는 두 변수 간의 상호작용 효과가 없다고 시사하는 것과 같다.
\[\begin{aligned} SS_{\text{비료, 토양}} &= 3(20-21-25+26)^2 + 3(30-31-25+26)^2 \\ &+ 3(25-26-25+26)^2 + 3(22-21-27+26)^2 \\ &+ 3(32-31-27+26)^2+3(27-26-27+26)^2 \\ &= 0 \end{aligned}\] -
오차 분산 계산
$SS_E$ 는 각 표본 내에서의 분산의 합을 의미하게 된다. 위 예시에서는 각 표본의 분산은 모두 $2$로 동일한 값을 갖기 때문에 전체 합산한 결과 $SS_E=12$ 의 결과를 얻을 수 있다. 이어서 자유도로 나눈 결과인 $MS_E$ 는 $SS_E$ 를 $18-32=12$ 로 나눈 $1$이 된다.
최종적으로 비료에 대한 f-value는 150, 토양에 대한 f-value는 18, 상호작용에 대한 f-value는 0임을 구하였다. f-table에 따르면 독립 변수 ‘비료’의 자유도는 2이었고, 전체 집단의 자유도는 12이므로 critical value는 9.41 값이 된다. 비료의 f-value는 critical value를 훨씬 넘는 값이므로 비료로 인해 표본의 평균차이가 유의미함을 확인하였고 마찬가지로 토양과 상호작용에 대해서도 판단할 수 있을 것이다.
Multivariate ANOVA
이원분산분석을 다원분산분석으로 확장하면, 세 개 이상의 독립 변수를 동시에 고려할 수 있다. 하지만 변수 간의 상호작용이 기하급수적으로 늘어나 계산이 복잡해지는 단점이 있다. 이러한 이유로, 다원분산분석보다는 회귀분석을 사용하는 경우가 많다. 회귀분석은 변수별로 결과에 미치는 영향을 정량화할 수 있어 더욱 유용하다.
Summary
일원 분산분석과 이원 분산분석을 중점적으로 설명하면서 결국 하고 싶었던 것은 표본 집단에서 보이는 표본 평균의 차이가 유의미한지 보이는 것이었다. 다시 말해, 독립변수의 설정으로 인해 표본 평균의 변화가 의미 있었는지, 독립변수가 종속변수에 큰 영향을 보이는지 보는 통계적 검정방법이었다. 일원 분산 분석의 경우 각 집단 내의 분산 그리고 집단 간 분산의 비율을 통해 f-value를 구했다면 이원 분산분석은 여기에 더해 두 독립변수 사이의 상호작용까지 고려한다는 점에서 차이를 보였다.
머신러닝을 공부하는 나로서는 독립변수가 단순히 2개가 아닌 많게는 50개 까지도 동시에 고려하는 경우가 많이 생긴다. 처음 머신러닝의 시작이 회귀분석으로 시작했던 반면, 통계적 검정 기법인 T-Test 그리고 ANOVA 까지 살펴보면서, 각 변수의 중요도를 확인할 수 있는 통계적 기법이 있다는 사실을 깨닫게 해주었다. 수식적으로 하나씩 의문을 품으면서 공부를 진행하게 되어 많은 시간이 소모되었지만, 배움이 많았던 주제라고 생각된다.




Start the conversation