Table of Contents
학부과정에서 확률통계와 머신러닝을 학습했음에도 불구하고, ANOVA라는 개념은 나에게 꽤 낯설게 다가왔던 용어 중 하나였다. 이번 글에서는 ANOVA가 무엇인지 살펴보고, 그동안 별도로 학습한 내용을 정리해 보려고 한다.
T-Test & ANOVA
ANOVA(Analysis of Variance)는 한국말로 ‘분산분석’이라고 한다. 말 그대로 분산을 분석한다는 뜻인데, 여기서 어떤 분산을 분석하고 무엇을 알아내고자 하는지부터 시작해 보려고 한다.
이전 글에서는 T-Test에 대해 다뤘다. 간략히 말하자면, T-Test는 두 개의 표본 집단에서 얻은 평균 차이가 우연히 발생한 것인지 검증하는 방법이다. 표준 오차(SE, Standard Error)를 사용해 t-value를 도출하고, 이를 통해 차이가 유의미한지 판단한다. ANOVA는 이러한 T-Test를 확장한 방법이라고 볼 수 있다. 두 개의 표본 집단이 아니라, 세 개 이상의 표본 집단에서 평균 차이가 우연히 발생한 것인지 검증하는 통계적 기법이다.
Necessity of ANOVA
표본 집단이 세 개라면, 각 표본 집단 쌍에 대해 T-Test를 세 번 수행해 차이가 유의미한지 판단해볼 수도 있다. 그러나 이렇게 하면 1종 오류(Type I Error)가 누적되는 문제가 발생한다. 일반적으로 p-value를 0.05로 설정해, 실제로 차이가 없는데도 차이가 있다고 판단할 확률을 5%로 제한한다. 하지만 T-Test를 세 번 반복하면 이 확률이 누적되어 약 15%에 달하게 된다. (정확히는 $1-(0.95)^3$ 만큼 누적된다.) 이런 문제를 해결하기 위해 ANOVA가 고안되었다.
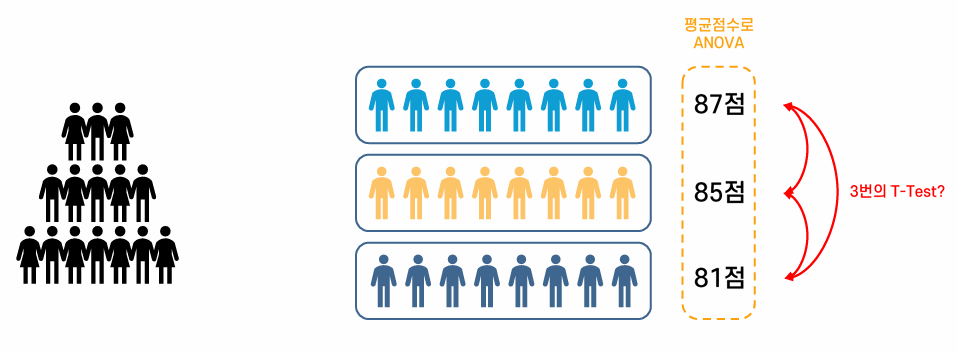각 학습방법에 따른 평균의 차이에 대해 T-Test를 적용
T-Test에서는 각 집단의 평균 차이를 표준 오차로 분석했다면, ANOVA는 각 집단의 분산을 분석한다. 집단 내 분산이 작고, 집단 간 차이가 크다면 두 집단은 확실히 다르다고 판단할 수 있다. 그래서 각 집단의 분산을 기준으로 검증하는 이 방법을 ‘분산분석’이라고 부른다. ANOVA의 종류를 나누는 기준인 변수에 대해 먼저 살펴본 뒤, 본격적으로 ANOVA를 알아보자.
Variables
통제 변수, 독립 변수, 종속 변수
실험을 진행하는 연구자라면 이런 변수들에 익숙할 것이다. 반면, 주로 코드를 통해 결과를 얻는 사람에게는 낯설게 느껴질 수 있다. 이를 쉽게 설명하기 위해 ‘식물 키우기’ 실험을 예로 들어보자.
독립변수, 통제변수, 종속변수의 예시
식물이 성장하는 데 영향을 미치는 요소로 일조량, 토양, 비료가 있다고 하고, 여기서 비료에 따라 식물의 높이가 얼마나 달라지는지 알아보고 싶다면, 변수들은 다음과 같이 분류된다.
통제 변수: 실험에서 변화시키지 않는 변수들 (예: 일조량, 토양) 독립 변수: 실험에서 변화시키는 원인 (예: 비료) 종속 변수: 실험 결과로 관찰하고자 하는 값 (예: 식물 높이)
ANOVA에서는 변화시키는 독립 변수의 개수에 따라 일원분산분석, 이원분산분석, 그리고 그 이상의 다원분산분석으로 나눈다. 우선 단순한 일원분산분석을 기준으로 설명을 이어가겠다.
One-way ANOVA
일원분산분석은 각 표본 집단의 집단 내 분산과 집단 간 분산을 고려해, 독립 변수에 의해 실험 결과가 유의미하게 달라졌는지를 검증하는 방법이다. 개인적으로는 이 과정이 머신러닝의 클러스터링 기법과 유사하다는 느낌을 받았다.
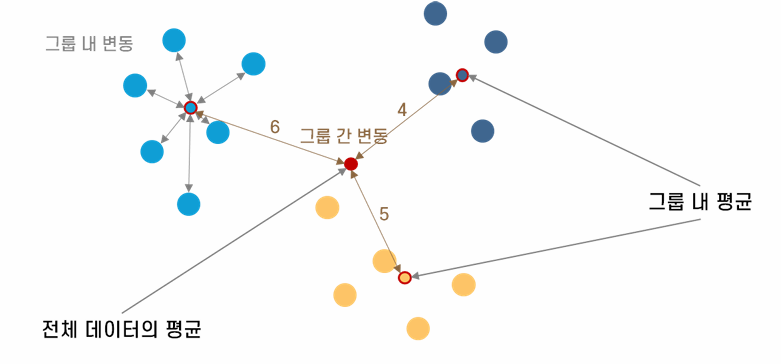Within variance and between variance
Within variance
집단 내 분산은 각 데이터가 집단 평균으로부터 얼마나 떨어져 있는지를 측정한다. 수식은 다음과 같다.
\[\text{within variance} = \frac{\sum_{i=1}^{k}\sum_{j=1}^{n_i} (x_{i, j} - \bar{x}_i)^2}{N - k}\]Between variance
집단 간 분산은 각 집단 평균이 전체 평균과 얼마나 다른지를 측정한다. 여기서는 각 집단의 데이터 수를 가중치로 사용한다. 수식은 다음과 같다.
\[\text{between variance} = \frac{\sum_{i=1}^{k} n_k (\bar{x}_k - \bar{x})^2}{k - 1}\]F-value
ANOVA는 집단 내 분산과 집단 간 분산의 비율을 비교해 유의미성을 판단한다. 이 비율은 다음과 같다.
\[\text{f-value} = \frac{\text{between variance}}{\text{within variance}}\]이후 과정은 T-Test와 비슷하다. 적절한 p-value를 설정하고, f-table에서 임계값(critical value)을 찾아 단측 검정을 진행한다. ANOVA는 항상 단측 검정만 사용하는데, 이는 분산의 비율이 음수가 될 수 없기 때문이다.
Example: One-way ANOVA
3개의 비료(A, B, C)가 식물 성장에 미치는 영향을 유의수준 0.05에서 검증하는 예제를 살펴보자.
| 비료 | A 그룹 | B 그룹 | C 그룹 |
|---|---|---|---|
| 집단 내 식물의 높이 | 20, 21, 19 | 30, 29, 31 | 25, 24, 26 |
먼저 각 그룹에 대한 within variance를 계산해보면 아래와 같다:
- 집단 A의 오차제곱합: $0 + 1 + 1 = 2$
- 집단 B의 오차제곱합: $0 + 1 + 1 = 2$
- 집단 C의 오차제곱합: $0 + 1 + 1 = 2$
이어서 집단 간 분산값인 between variance를 계산해보자. 전체 그룹에 대대한 평균 값 $\bar{x}$ 는 25이며, 각 집단 내 평균은 $\bar{x}_A=20$, $\bar{x}_B=30$, $\bar{x}_C=25$ 로 구성된다. 그리고 집단 내 데이터의 수는 모두 $3$ 으로 동일하다. 이것들을 기반으로 위 수식에 그대로 대입하게 되면 집단 간 분산 값을 획득할 수 있다.
\[\therefore \text{between variance} = \frac{3(20-25)^2 + 3(30-25)^2 + 3(25-25)^2}{3-1} = 75\]끝으로 집단 간 분산을 집단 내 분산으로 나눈 값을 계산해주면 f-value는 $\frac{75}{1}$ 의 75가 된다. F-table에서 자유도(df) 2와 6에 해당하는 임계값(critical value)은 5.1433이다. 구한 F-value(75)가 이 값을 훨씬 초과하므로, 비료에 따라 식물 성장에 차이가 있음을 알 수 있다.
여기서 중요한 특징은 우리는 하나의 독립 변수(비료)의 카테고리(A, B, C) 중 유의미한 차이를 보이는 집단이 있다는 것을 확인하였으나, 정확히 어떤 집단에 차이가 있다는 것을 밝히지는 못하였다. 따라서 ANOVA 이후, 정확히 어떤 집단에 차이가 발생했는지 확인하기 위해서는 사후 검정(post-hoc) 과정이 필수적이다.
Summary
이번 글에서는 ANOVA의 기본 개념과 일원분산분석(One-way ANOVA)에 대해 알아보았다. ANOVA는 세 개 이상의 집단 간 평균 차이를 검증하는 데 매우 유용한 통계 기법이다. 특히, T-Test로는 해결할 수 없는 다중 비교 문제를 효과적으로 해결할 수 있다는 점에서 그 중요성이 크다. 일원분산분석을 통해 우리는 독립 변수의 변화가 결과에 유의미한 영향을 미치는지 판단할 수 있었지만, 그 차이를 구체적으로 분석하기 위해서는 사후 검정(post-hoc test)이 필요하다는 점도 알 수 있었다.
다음 글에서는 이원분산분석 (Two-way ANOVA)과 다원분산분석 (Multivariate ANOVA)을 다룰 예정이다. 이원분산분석에서는 두 개의 독립 변수가 결과값에 어떻게 상호작용하는지를 분석하며, 다원분산분석에서는 더 복잡한 상황에서의 통계적 검증 방법을 알아볼 것이다. 마지막으로 ANOVA의 전반적인 내용을 정리하며 실제로 데이터를 분석할 때 어떤 점을 고려해야 하는지까지 다뤄보겠다.
Start the conversation